Albert Einstein once said “Compound interest is the 8th wonder of the world. He who understands it, earns it; he who doesn’t, pays it.”
Despite this awesome quote, compound interest remains one of the more misunderstood concepts. In fact, when I asked on Twitter, the vast majority of replies involved compound interest.
We don’t have statistics on whether this is true… but it feels like it’s true.
But the reality is that the power of compound interest is more than math and money. The power of compound interest is not in actual interest but in what it means for you, relationships, and how to amass wealth.
We will first discuss the math and follow it up with how it applies to life.
Table of Contents
What is Compound Interest?
If you don’t fully grasp why compound interest is so important, don’t worry. You are not alone.
When I asked Twitter for the one financial concept most people don’t understand, the most common answer was compound interest.
Compound interest is the interest calculated on your principal and the accumulated interest of all the previous periods. The instrument will document how often it compounds – annually, semiannually (2x a year), quarterly, monthly, daily, or continuously. It’s compounding because the amount builds on itself. It’s powerful because, over time, a small amount can accumulate to a much larger one if you do not withdraw anything.
The other version of interest is known as simple interest. With simple interest, you only earn interest on the principal and not on any accrued interest from previous periods. If you have an asset that generates interest and that interest gets deposited or transferred to another account, then you’re usually looking at simple interest.
Most deposit products, like a certificate of deposit, use compound interest.
Compound Interest Formula
To calculate the earnings on an asset given its interest rate, period, and time – use this equation:
Where:
- FV = Future Value
- PV = Present Value
- n = compounding periods per year
- i = interest rate
- t = time in years
Continuous Compound Interest Formula
Continuous compounding is a special case because you calculate interest based on an infinite number of periods, which mathematically involves limits – you can look it up but it’s just this equation:
Where:
- FV = Future Value
- PV = Present Value
- e ≈ 2.7183 (it’s a mathematical constant)
- i = interest rate
- t = time in years
(and you don’t really need the equation, you can use a simple compound interest calculator to do the math)
It’s such a simple idea but it’s powerful – so why do so few people understand it?
Why don’t people “get” compound interest?
There is a powerful quote that illustrates the fundamental reason why some people fail to understand (and take advantage of) compound interest.
It’s been said by many people but the time I saw it, and when it took residence in my brain, was when Bill Gates wrote in the Afterword of his book The Road Ahead:
We always overestimate the change that will occur in the next two years and underestimate the change that will occur in the next ten. Don’t let yourself be lulled into inaction.
He was referring to the growth of technology and the internet.
It’s always hard to see something that isn’t there. It’s even harder to see something that will be there in the future. This is why real estate agents stage a house before they show it. Even seeing other people’s furniture in an empty room is better than seeing an empty room because at least you’re seeing something.
If a room is hard to picture, can you imagine trying to envisage your life in five years? Ten years? A few years ago, Merrill Edge released a face aging app that helped people better see their future. It was gimmicky and it just showed you an older face, which was probably not what your face would look like then, but it’s like staging a house. Your oldish face was better than not seeing a version of your future face.
That’s why people have trouble understanding the power of compounding interest.
We are terrible at seeing the future!
Let’s Help You Visualize Compound Interest
Part of the trouble is that we’re also just looking at numbers. The numbers are abstract. You don’t have nine. You have nine of something.
What does $1,000 look like when you give it a 5% compounding interest rate for forty years?
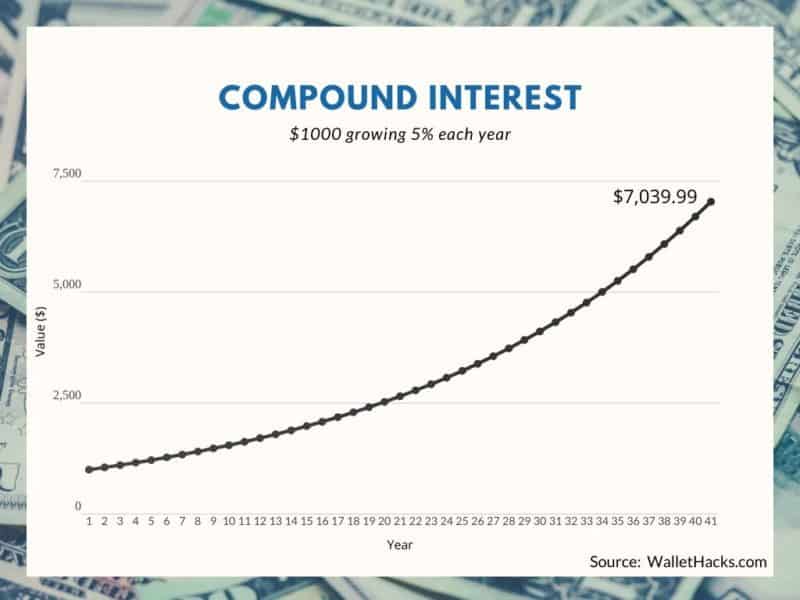
What if you start with $1,000 and give it a 5% compound interest PLUS you add a $1,000 contribution each year?
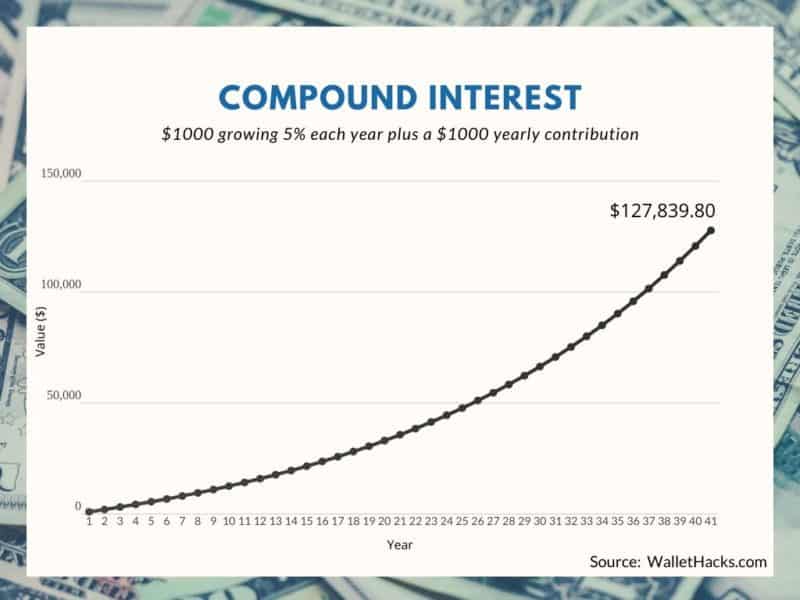
Of course, the second chart is much bigger, you’ve contributed $41,000 over forty years versus just $1,000 – but it highlights why compounding interest is so powerful.
But a chart is still just a chart. It’s just a line with some numbers. It’s hard to SEE.
How can we put this into terms you’ll appreciate?
What if you calculated how many hours you would need to work to make up the difference between what you’ve accumulated and what you’ve contributed? In the second chart, you’ve contributed $41,000 but you’ve amassed a nest egg of almost $128,000 – a difference of $87,000.
How many hours do you have to work to get $87,000? If you don’t know your rough hourly rate but are paid a salary, just divide your annual salary by 2,000. That’s 50 weeks of work, assuming two weeks of vacation, and a close enough approximation.
If you earn $50,000 – you earn $25 per hour. $87,000 = 3,480 hours or 435 days or work.
If you earn $100,000 – you earn $50 per hour. $87,000 = 1,740 hours or 217.5 days or work.
It’s easier to see an extra year of work, right?
If you need more of a visual… $87,000 is also four 2020 Toyota Corollas:

Or you can take 86 people on this cruise to Alaska (or go on it 86 times!):
The opportunities to spend $87,000 are endless!
How Compounding Applies to Life
If you didn’t know the math before the boring equation, understanding how the numbers work probably doesn’t resonate with you. I don’t blame you. Numbers are antiseptic.
But give me a moment and I’ll explain how compounding applies to life.
Think about your closest and strongest relationships – when did you meet them? How much time, cumulatively, have you spent with them?
If you’re like most people, the people you are closest too are the ones you’ve spent the most time with. You may have met them a long time ago or more recently, but the theme is how much time you’ve spent together. The intensity of that time matters too.
Your parents. Your childhood friends. Your college friends.
Consider this – your relationship has compounded over a long period of time. Small interactions, like a small percentage of interest, accumulate over many years.
When asked, Robert Waldinger, the director of the Harvard Study of Adult Development where they tracked the lives of 724 men throughout their lives, said that one of the most important factors in determining happiness was the closeness of your relationships. Waldinger’s TED talk is only 13 minutes and one of my favorites.
The reason why your relationships strengthen over time is that you accumulate memories together. You build trust over multiple instances where you need to trust one another. You were stuck in traffic on the way back home and they picked your kids up at the bus stop. You forgot to close your garage door so they stopped by to his the button for you. A massive maple tree fell and you helped clear it.
Over time, these moments build on one another much like compound interest. In the end, your relationship is stronger. It’s compounded.
Some of my closest friends are those I’ve met through the internet. We have worked together on projects, brainstormed on phone calls, and spent time together in person chopping it up over adult beverages. The cumulative time I’ve spent with them in person might be less than a week. But with the internet and messaging, it’s easy to communicate and interact with someone for a long period without actually being in each other’s presence. Those microtransactions build relationships despite the contact being quite minimal.
I’ll leave you with one final example from someone I met years ago before he became the guru of habits because it explains exactly this principle but in a different realm. James Clear’s article on Continuous Improvement explains how 1% improvement seems so so small but over time can be massive (he didn’t always write about habits but he was always pretty rock solid with words).
This chart is about continuous improvement but it’s really about compound interest too:
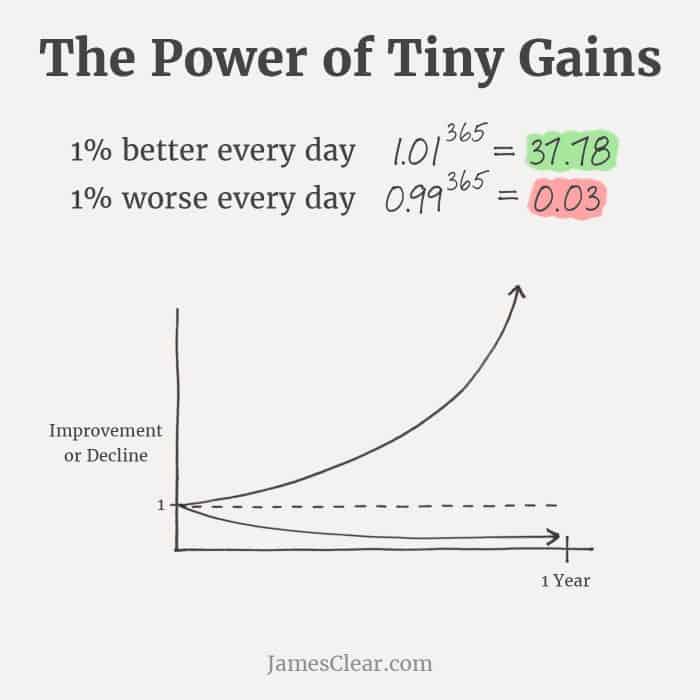
So, as you go through your day, think about compound interest and how it permeates so much of our lives, not just our money.




Ally says
Powerful reminder and perfect “timing” considering the current madness. We all know the right thing to do in times like this, but emotions are at times stronger than common sense. It’s good to see reassuring articles such as this one. Thanks Jim!
It’s hard to do the “right thing” when you’re stressed!
Alien on F.I.R.E. says
Great post and Waldinger’s TED Talk is one of my favourites as well!
It’s so insightful and counterintuitive to what marketing tells us! We all need expensive cars, big houses, and yachts to be happy!
David Ferencz says
One thing that you didn’t note your in your $87,000 consideration is that it’s 435 days (or 217.5 days) of your gross salary not your net and without expenses. That $87,000 comes to a lot more time worked, once you add in all the real expenses and taxes that a person would have to pay.
Compound interest rocks!
Very true!
Anne says
Re dividends: what about reinvesting the stocks vs taking the cash? In scary times it feels safer to take the cash payout – or is it better to reinvest in the stock shares?
I invest on a regular basis (automated investments that I set up in Vanguard) and so I take the dividends as cash. I think it makes it easier from a tax filing perspective because you don’t have all those little tax lots floating around. But if you don’t invest on a regular basis, automatic dividend reinvestment is a good idea.
Louise says
I’d like to see an article about compound interest when it refers to debt.
What do you mean?
Budget Life List says
I prefer concepts that are fluid to the various aspects of our lives. Compound interest falls into this category though I have never thought about it, until I read this post! I have always associated it as a “finance area only”. Ironically, I just read The Slight Edge and it seems eerily familiar!
A lot of folks do just think of it with respect to interest but it’s everywhere!